Educação

São raríssimos os amantes da música. Se você é um deles, tente não se deprimir ao ler este texto.
Devo avisar também que não sou um especialista em música, apesar de me considerar um entusiasmado apreciador de obras de compositores e instrumentistas como Vangelis, Mike Oldfield, Rick Wakeman e Jean Michel Jarre, entre muitos outros. Contei com a ajuda do músico Don Healy para escrever esta postagem, ao qual evidentemente agradeço. Peço ao leitor para encarar este texto como um ensaio meramente especulativo, no qual se assume que as atuais civilizações humanas ainda podem durar muito tempo, mantendo registros de músicas.
Nos parágrafos que se seguem argumentamos que há limites na arte da composição musical. Levamos em conta elementos matemáticos da teoria da música, bem como limitações auditivas do ser humano.
Na música ocidental, como é tradicionalmente conhecida, convencionam-se doze notas. São sete as notas naturais: Dó, Ré, Mi, Fá, Sol, Lá e Si (em ordem crescente de frequências dominantes). As demais são conhecidas como acidentes: os sustenidos de Dó, Ré, Fá, Sol e Lá, os quais coincidem com os bemóis de Ré, Mi, Sol, Lá e Si, respectivamente. Podemos esquematizar todas essas notas em uma linha reta (ordenada por frequências dominantes), conforme a imagem abaixo.
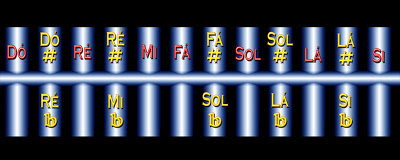
O símbolo # denota sustenido. O símbolo b denota bemol. As notas naturais correspondem à teclas brancas de um piano ou teclado. Já os acidentes são reproduzidos pelas teclas negras.
A essas doze notas podem ser acrescentadas outras para a esquerda ou para a direita, caracterizando diferentes oitavas, conforme a figura abaixo. Uma oitava é uma sequência de todas as notas de um dó até o próximo dó.
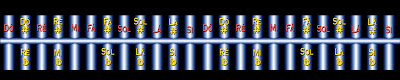
A inserção de notas não é arbitrária pois, além de ser sequencial, também depende da capacidade de audição de quem escutará a música. Como todo ser humano tem uma capacidade limitada de audição, a quantia de notas possíveis é finita.
A distância entre duas notas quaisquer é chamada de intervalo. Alguns autores, no entanto, assumem que um intervalo é um conjunto de duas notas. Para nossos propósitos assumimos nossa própria definição de intervalo. A distância (intervalo) entre qualquer nota e uma nota imediatamente à esquerda ou à direita é sempre meio tom. Por exemplo: o menor intervalo entre um Dó e um Dó sustenido é meio tom; o menor intervalo entre um Dó e um Ré é um tom; o menor intervalo entre um Ré e um Sol é dois tons e meio; e assim por diante.
O conjunto de notas, munido de uma função que determina os intervalos entre elas, corresponde àquilo que os matemáticos chamam de modelo de espaço métrico. Isso porque intervalos nada mais são do que distâncias entre as notas, no sentido matemático usual. O leitor que não estiver familiarizado com o conceito de espaço métrico não deve se assustar. Basta perceber, intuitivamente falando, as notas como pontos em um segmento de reta, de modo que a menor distância não nula entre esses pontos é sempre meio.
Uma música pode ser definida a partir de uma sequência de intervalos. Ou seja, qualquer música ocidental pode ser identificada como uma sequência de números racionais que são múltiplos inteiros de meio. Este é um aspecto extremamente importante e nem sempre compreendido entre músicos! Não são sequências de notas que definem músicas, mas sim sequências de intervalos.
Uma vez definida uma sequência de intervalos, o compositor usualmente define também um ritmo e uma tônica para a sua música. A tônica é a primeira nota de uma escala. E uma escala é uma sequência escolhida de notas (entre as doze disponíveis). Frequentemente as escalas da música ocidental empregam oito notas. É claro que a primeira nota da música não precisa ser a tônica. Mas a primeira nota certamente deve estar na escala definida a partir da tônica. E, literalmente, a primeira nota da música pode ser qualquer uma entre aquelas disponíveis na escala definida pela tônica.
O ritmo tem o propósito de estabelecer a proporcionalidade da distância temporal entre as notas executadas através de instrumento ou canto. Já o andamento define a velocidade de execução de uma música. Portanto, conhecendo o ritmo e o andamento, podemos determinar o momento exato em que cada nota é executada, a partir da primeira.
Questões sobre mudança de tonalidade ou quebra de ritmo (muito comuns em peças musicais mais elaboradas) são discutidas ao final desta postagem.
Você leitor já deve ter visto em espetáculos de música pop algum instrumentista ou cantor perguntar aos colegas qual é o tom da música, antes de iniciar a execução. O que este artista quer saber, na verdade, é a primeira nota da escala (a tônica). Isso porque uma mesma música (sequência de intervalos) pode ter diferentes tonalidades (tônicas). Mudar a tonalidade não altera a música. Analogamente, mudanças de arranjo instrumental ou de velocidade (andamento) em uma mesma sequência de intervalos não caracterizam músicas distintas. Quando um leigo ouve With a Little Help From My Friends na versão original dos Beatles, pode ter a sensação de que se trata de outra música, ao escutar o arranjo de Joe Cocker para a mesma composição. Mas não é o caso, apesar de ambas as versões terem andamentos e arranjos diferentes.
Portanto, dada a limitação auditiva humana, existe uma quantia finita de tonalidades. E isso vale para qualquer música.
É claro que não há limites sobre o número de intervalos que definem uma música, assim como não há limites no número de frases que podem ser escritas em um livro. No entanto, qualquer ouvinte (e músicas são destinadas a ouvintes!) dispõe de tempo limitado para ouvir qualquer música. Além disso, há limites também sobre o andamento da peça musical. O guitarrista John Taylor, por exemplo, consegue executar Flight of the Bumblebee (célebre peça de Rimsky Korsakov, originalmente escrita para um andamento de 170 batidas por minuto), na velocidade recordista de 600 bpm. Taylor foi para o Guiness World Records, por conta desta espetacular proeza. Vale observar que as 170 batidas originais não representam 170 notas tocadas em um espaço de um minuto, mas que existem 170 tempos dentro desse mesmo espaço. E ainda assim a execução de Taylor (possível graças a décadas de treino) mal permite reconhecer a música. Mesmo que fosse possível a execução de milhares ou milhões de notas por segundo, o som resultante soaria como um ruído branco para qualquer ouvido humano. Portanto, levando em conta a limitada disponibilidade de tempo de qualquer ouvinte, bem como a sua limitada capacidade neurológica e auditiva de assimilação musical, fica claro que existe uma quantia finita de possíveis sequências de intervalos. Em outras palavras, existe uma quantia finita de possíveis composições musicais.
Uma música que é executada em uma única tonalidade e um único ritmo, do início ao fim, pode ser comparada a uma sequência de intervalos obtida a partir de uma linha reta, como já ilustramos acima. Se o compositor optar por uma mudança de tonalidade, ele age como se estivesse saltando para uma segunda reta paralela, em uma superfície plana, conforme a imagem abaixo.
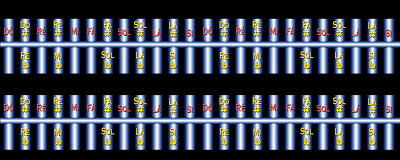
Apesar disso, os limites físicos e fisiológicos apontados anteriormente continuam sendo válidos. Ainda estamos confinados ao tempo disponível para apreciação da música e à capacidade de assimilação de notas por unidade de tempo. O fato de haver tais limites não se altera, mesmo que consideremos a possibilidade de inserção de acordes e arpejos em uma composição musical.
Os fãs de guitarras elétricas poderiam argumentar que o emprego de slides permite explorar sons intermediários entre notas, conferindo uma sonoridade diferente e mais ampla. No entanto, qualquer música executada com o auxílio de um slide pode ser também executada sem este artifício. Slides não mudam músicas.
Do ponto de vista puramente matemático, não há limites sobre possíveis ritmos. É claro que os ritmos mais usuais na música são o 4/4 (como no rock'n roll e no blues, entre outros), o 2/4 (folclore britânico e jazz, entre outros) e o 3/4 (country e valsa, entre outros). No entanto, ritmos exóticos (como o 32/64 adotado por George Harrison em algumas de suas composições fortemente influenciadas pela música indiana) não são percebidos por leigos como algo muito diferente do 4/4. Mesmo músicos profissionais experientes raramente percebem essa diferença. E mais raros ainda são aqueles que conseguem executar tais ritmos extravagantes.
Apesar do ritmo 6/8 não ser equivalente ao ritmo 3/4 (o que explica porque esta notação em forma fracionária é rejeitada por muitos músicos), a quantia de ritmos humanamente executáveis e humanamente diferenciados por ouvintes também é finita. Além disso é extremamente discutível se ritmos distintos definem músicas distintas.
Logo, a música ocidental apresenta limitações quanto à quantia de possíveis composições. Isso significa que o fim da música, como hoje a compreendemos, é simplesmente inevitável.
Músicas orientais, como a indiana, obedecem a regras muito distintas daquelas que apresentamos acima. Mas ainda contam com limitantes definidos por escalas discretas e, portanto, contáveis. E igualmente contam com limitantes fisiológicos de instrumentistas e ouvintes.
O professor e pesquisador Armand Leroi, do Imperial College em Londres, anunciou na BBC News que acredita ser possível conceber uma máquina que compõe músicas a partir de caos sonoro. Em artigo publicado em 2012 no Proceedings of the National Academy of Sciences (EUA), Leroi e colaboradores discutem sobre um programa de computador que concebe populações inteiras de frases musicais a partir de um mecanismo Darwiniano de reprodução, evolução e adaptação. Ele acredita que no futuro compositores humanos serão completamente desnecessários.
Esta é uma forma ironicamente poética de reconhecer que uma música é um ser vivo e que, portanto, nasce, cresce, se reproduz, evolui e morre. No entanto, se um compositor humano se sente sem inspiração para conceber algo genuinamente novo, ele ainda poderá contar com a inseminação artificial de Leroi e colaboradores. A possível desvantagem deste tipo de iniciativa, porém, é que ela pode nos trazer o fim da música muito mais rapidamente.
- Algumas Curiosidades Lógicas
Nesta postagem não há tema novo algum. Tudo aqui se refere a assuntos muito conhecidos na literatura especializada. No entanto, como vejo inúmeros discursos e textos de matemática no Brasil que fazem consideráveis confusões de caráter lógico,...
- Como Você Se Relaciona Com As Artes?
Então, você pode responder a essa pergunta? Não é difícil, note que tudo a sua volta, ou melhor, o mundo que te rodeia está impregnado de cores e formas. As cores são usadas para tudo, desde roupas até o acabamento dos imóveis, móveis e automóveis....
- 8º Ano, Tá Ai O Conteúdo.
8º ano – 1º bimestre: Artes Visuais · Compreender a presença da arte no Brasil Colônia. · Perceber a singularidade da estética barroca, a partir...
- Galera Do 7º Ano, Anota Ai As Novidades
Então, no post anterior eu coloquei os conteúdos mínimos exigidos pela secretaria de educação do Estado do Rio de Janeiro para o 6º ano, continuando a nossa atualização eu coloco aqui o conteúdo de 7º ano. Na minha opinião essas mudanças foram...
- Crítica: Exposição De Notas Bimestrais Na Sala De Aula.
Trabalho de Artes – Ciep 280 Grupo: João Pedro Freitas, João Pedro dos Anjos, Kelvin, Tharlaynny, Victória e Thalita.Bom, quem nunca perguntou sua nota do bimestre ao professor?Todo mundo já fez isso, mas, muitas vezes, nós ocupamos a cabeça dos...
Educação
Quando Será o Fim da Música?

São raríssimos os amantes da música. Se você é um deles, tente não se deprimir ao ler este texto.
Devo avisar também que não sou um especialista em música, apesar de me considerar um entusiasmado apreciador de obras de compositores e instrumentistas como Vangelis, Mike Oldfield, Rick Wakeman e Jean Michel Jarre, entre muitos outros. Contei com a ajuda do músico Don Healy para escrever esta postagem, ao qual evidentemente agradeço. Peço ao leitor para encarar este texto como um ensaio meramente especulativo, no qual se assume que as atuais civilizações humanas ainda podem durar muito tempo, mantendo registros de músicas.
Nos parágrafos que se seguem argumentamos que há limites na arte da composição musical. Levamos em conta elementos matemáticos da teoria da música, bem como limitações auditivas do ser humano.
Na música ocidental, como é tradicionalmente conhecida, convencionam-se doze notas. São sete as notas naturais: Dó, Ré, Mi, Fá, Sol, Lá e Si (em ordem crescente de frequências dominantes). As demais são conhecidas como acidentes: os sustenidos de Dó, Ré, Fá, Sol e Lá, os quais coincidem com os bemóis de Ré, Mi, Sol, Lá e Si, respectivamente. Podemos esquematizar todas essas notas em uma linha reta (ordenada por frequências dominantes), conforme a imagem abaixo.

O símbolo # denota sustenido. O símbolo b denota bemol. As notas naturais correspondem à teclas brancas de um piano ou teclado. Já os acidentes são reproduzidos pelas teclas negras.
A essas doze notas podem ser acrescentadas outras para a esquerda ou para a direita, caracterizando diferentes oitavas, conforme a figura abaixo. Uma oitava é uma sequência de todas as notas de um dó até o próximo dó.

A inserção de notas não é arbitrária pois, além de ser sequencial, também depende da capacidade de audição de quem escutará a música. Como todo ser humano tem uma capacidade limitada de audição, a quantia de notas possíveis é finita.
A distância entre duas notas quaisquer é chamada de intervalo. Alguns autores, no entanto, assumem que um intervalo é um conjunto de duas notas. Para nossos propósitos assumimos nossa própria definição de intervalo. A distância (intervalo) entre qualquer nota e uma nota imediatamente à esquerda ou à direita é sempre meio tom. Por exemplo: o menor intervalo entre um Dó e um Dó sustenido é meio tom; o menor intervalo entre um Dó e um Ré é um tom; o menor intervalo entre um Ré e um Sol é dois tons e meio; e assim por diante.
O conjunto de notas, munido de uma função que determina os intervalos entre elas, corresponde àquilo que os matemáticos chamam de modelo de espaço métrico. Isso porque intervalos nada mais são do que distâncias entre as notas, no sentido matemático usual. O leitor que não estiver familiarizado com o conceito de espaço métrico não deve se assustar. Basta perceber, intuitivamente falando, as notas como pontos em um segmento de reta, de modo que a menor distância não nula entre esses pontos é sempre meio.
Uma música pode ser definida a partir de uma sequência de intervalos. Ou seja, qualquer música ocidental pode ser identificada como uma sequência de números racionais que são múltiplos inteiros de meio. Este é um aspecto extremamente importante e nem sempre compreendido entre músicos! Não são sequências de notas que definem músicas, mas sim sequências de intervalos.
Uma vez definida uma sequência de intervalos, o compositor usualmente define também um ritmo e uma tônica para a sua música. A tônica é a primeira nota de uma escala. E uma escala é uma sequência escolhida de notas (entre as doze disponíveis). Frequentemente as escalas da música ocidental empregam oito notas. É claro que a primeira nota da música não precisa ser a tônica. Mas a primeira nota certamente deve estar na escala definida a partir da tônica. E, literalmente, a primeira nota da música pode ser qualquer uma entre aquelas disponíveis na escala definida pela tônica.
O ritmo tem o propósito de estabelecer a proporcionalidade da distância temporal entre as notas executadas através de instrumento ou canto. Já o andamento define a velocidade de execução de uma música. Portanto, conhecendo o ritmo e o andamento, podemos determinar o momento exato em que cada nota é executada, a partir da primeira.
Questões sobre mudança de tonalidade ou quebra de ritmo (muito comuns em peças musicais mais elaboradas) são discutidas ao final desta postagem.
Você leitor já deve ter visto em espetáculos de música pop algum instrumentista ou cantor perguntar aos colegas qual é o tom da música, antes de iniciar a execução. O que este artista quer saber, na verdade, é a primeira nota da escala (a tônica). Isso porque uma mesma música (sequência de intervalos) pode ter diferentes tonalidades (tônicas). Mudar a tonalidade não altera a música. Analogamente, mudanças de arranjo instrumental ou de velocidade (andamento) em uma mesma sequência de intervalos não caracterizam músicas distintas. Quando um leigo ouve With a Little Help From My Friends na versão original dos Beatles, pode ter a sensação de que se trata de outra música, ao escutar o arranjo de Joe Cocker para a mesma composição. Mas não é o caso, apesar de ambas as versões terem andamentos e arranjos diferentes.
Portanto, dada a limitação auditiva humana, existe uma quantia finita de tonalidades. E isso vale para qualquer música.
É claro que não há limites sobre o número de intervalos que definem uma música, assim como não há limites no número de frases que podem ser escritas em um livro. No entanto, qualquer ouvinte (e músicas são destinadas a ouvintes!) dispõe de tempo limitado para ouvir qualquer música. Além disso, há limites também sobre o andamento da peça musical. O guitarrista John Taylor, por exemplo, consegue executar Flight of the Bumblebee (célebre peça de Rimsky Korsakov, originalmente escrita para um andamento de 170 batidas por minuto), na velocidade recordista de 600 bpm. Taylor foi para o Guiness World Records, por conta desta espetacular proeza. Vale observar que as 170 batidas originais não representam 170 notas tocadas em um espaço de um minuto, mas que existem 170 tempos dentro desse mesmo espaço. E ainda assim a execução de Taylor (possível graças a décadas de treino) mal permite reconhecer a música. Mesmo que fosse possível a execução de milhares ou milhões de notas por segundo, o som resultante soaria como um ruído branco para qualquer ouvido humano. Portanto, levando em conta a limitada disponibilidade de tempo de qualquer ouvinte, bem como a sua limitada capacidade neurológica e auditiva de assimilação musical, fica claro que existe uma quantia finita de possíveis sequências de intervalos. Em outras palavras, existe uma quantia finita de possíveis composições musicais.
Uma música que é executada em uma única tonalidade e um único ritmo, do início ao fim, pode ser comparada a uma sequência de intervalos obtida a partir de uma linha reta, como já ilustramos acima. Se o compositor optar por uma mudança de tonalidade, ele age como se estivesse saltando para uma segunda reta paralela, em uma superfície plana, conforme a imagem abaixo.

Apesar disso, os limites físicos e fisiológicos apontados anteriormente continuam sendo válidos. Ainda estamos confinados ao tempo disponível para apreciação da música e à capacidade de assimilação de notas por unidade de tempo. O fato de haver tais limites não se altera, mesmo que consideremos a possibilidade de inserção de acordes e arpejos em uma composição musical.
Os fãs de guitarras elétricas poderiam argumentar que o emprego de slides permite explorar sons intermediários entre notas, conferindo uma sonoridade diferente e mais ampla. No entanto, qualquer música executada com o auxílio de um slide pode ser também executada sem este artifício. Slides não mudam músicas.
Do ponto de vista puramente matemático, não há limites sobre possíveis ritmos. É claro que os ritmos mais usuais na música são o 4/4 (como no rock'n roll e no blues, entre outros), o 2/4 (folclore britânico e jazz, entre outros) e o 3/4 (country e valsa, entre outros). No entanto, ritmos exóticos (como o 32/64 adotado por George Harrison em algumas de suas composições fortemente influenciadas pela música indiana) não são percebidos por leigos como algo muito diferente do 4/4. Mesmo músicos profissionais experientes raramente percebem essa diferença. E mais raros ainda são aqueles que conseguem executar tais ritmos extravagantes.
Apesar do ritmo 6/8 não ser equivalente ao ritmo 3/4 (o que explica porque esta notação em forma fracionária é rejeitada por muitos músicos), a quantia de ritmos humanamente executáveis e humanamente diferenciados por ouvintes também é finita. Além disso é extremamente discutível se ritmos distintos definem músicas distintas.
Logo, a música ocidental apresenta limitações quanto à quantia de possíveis composições. Isso significa que o fim da música, como hoje a compreendemos, é simplesmente inevitável.
Músicas orientais, como a indiana, obedecem a regras muito distintas daquelas que apresentamos acima. Mas ainda contam com limitantes definidos por escalas discretas e, portanto, contáveis. E igualmente contam com limitantes fisiológicos de instrumentistas e ouvintes.
O professor e pesquisador Armand Leroi, do Imperial College em Londres, anunciou na BBC News que acredita ser possível conceber uma máquina que compõe músicas a partir de caos sonoro. Em artigo publicado em 2012 no Proceedings of the National Academy of Sciences (EUA), Leroi e colaboradores discutem sobre um programa de computador que concebe populações inteiras de frases musicais a partir de um mecanismo Darwiniano de reprodução, evolução e adaptação. Ele acredita que no futuro compositores humanos serão completamente desnecessários.
Esta é uma forma ironicamente poética de reconhecer que uma música é um ser vivo e que, portanto, nasce, cresce, se reproduz, evolui e morre. No entanto, se um compositor humano se sente sem inspiração para conceber algo genuinamente novo, ele ainda poderá contar com a inseminação artificial de Leroi e colaboradores. A possível desvantagem deste tipo de iniciativa, porém, é que ela pode nos trazer o fim da música muito mais rapidamente.
loading...
- Algumas Curiosidades Lógicas
Nesta postagem não há tema novo algum. Tudo aqui se refere a assuntos muito conhecidos na literatura especializada. No entanto, como vejo inúmeros discursos e textos de matemática no Brasil que fazem consideráveis confusões de caráter lógico,...
- Como Você Se Relaciona Com As Artes?
Então, você pode responder a essa pergunta? Não é difícil, note que tudo a sua volta, ou melhor, o mundo que te rodeia está impregnado de cores e formas. As cores são usadas para tudo, desde roupas até o acabamento dos imóveis, móveis e automóveis....
- 8º Ano, Tá Ai O Conteúdo.
8º ano – 1º bimestre: Artes Visuais · Compreender a presença da arte no Brasil Colônia. · Perceber a singularidade da estética barroca, a partir...
- Galera Do 7º Ano, Anota Ai As Novidades
Então, no post anterior eu coloquei os conteúdos mínimos exigidos pela secretaria de educação do Estado do Rio de Janeiro para o 6º ano, continuando a nossa atualização eu coloco aqui o conteúdo de 7º ano. Na minha opinião essas mudanças foram...
- Crítica: Exposição De Notas Bimestrais Na Sala De Aula.
Trabalho de Artes – Ciep 280 Grupo: João Pedro Freitas, João Pedro dos Anjos, Kelvin, Tharlaynny, Victória e Thalita.Bom, quem nunca perguntou sua nota do bimestre ao professor?Todo mundo já fez isso, mas, muitas vezes, nós ocupamos a cabeça dos...
