Educação

Em documento redigido no dia 12 de janeiro de 1932, o canadense John Charles Fields propôs que "duas medalhas de ouro sejam entregues por ocasião de sucessivos Congressos Internacionais de Matemática, como forma de reconhecimento de conquistas significativas em matemática. Por conta da multiplicidade de ramos desta área e levando em conta o fato de que o intervalo entre tais congressos é de quatro anos, pelo menos duas medalhas deveriam ser entregues." Fields ainda complementa seu documento, afirmando que esta medalha não deveria ser apenas um reconhecimento de trabalho já realizado, mas também "um encorajamento para o ganhador investir em pesquisas futuras, bem como um estímulo para o esforço renovado dos demais."
Pois bem. A primeira Medalha Fields, hoje reconhecida como o mais importante prêmio em matemática, foi outorgada em 1936 para Lars Ahlfors (Finlândia) e Jesse Douglas (Estados Unidos). A última foi concedida este ano para Maryam Mirzakhani (Irã), Martin Hairer (Áustria), Manjul Bhargava (Canadá, Estados Unidos) e Artur Ávila (Brasil, França). Ao longo de 78 anos de premiação para 56 matemáticos de 21 países (Finlândia, Estados Unidos, França, Noruega, Japão, Reino Unido, Suécia, Rússia, Itália, Bélgica, China, Alemanha, Ucrânia, Nova Zelândia, África do Sul, Austrália, Israel, Vietnã, Áustria, Irã e Brasil), o que se pode dizer sobre os sonhos de John Charles Fields? A Medalha Fields cumpre com o papel idealizado pelo seu criador? Esta é uma daquelas perguntas que não se responde com um simples sim ou não.
Em artigo a ser publicado em 2015 no periódico Journal of Human Resources, George J. Borjas (Harvard University) e Kirk B. Doran (University of Notre Dame) promovem uma detalhada análise do impacto da Medalha Fields sobre aqueles que conquistaram este importante prêmio. Para o leitor interessado em uma versão preliminar deste artigo, basta clicar aqui.
As conclusões de Borjas e Doran certamente abrem espaço para discussões aprofundadas até mesmo sobre os méritos da meritocracia. Daí a importância deste artigo. Estes autores avaliaram a produtividade científica de um universo de 72 mil matemáticos espalhados pelo mundo, de acordo com banco de dados da American Mathematical Society, que leva em conta profissionais com pelo menos vinte anos de experiência.
Por um lado, a média de produção científica de matemáticos é inferior a 32 artigos durante toda a carreira. Por outro lado, medalhistas Fields publicam acima de 116 artigos durante a vida profissional. Mas, curiosamente, os matemáticos concorrentes que não conquistaram este prêmio apresentam uma produção média ligeiramente superior, com 126 artigos. Até aí, esses números pouco revelam. O resultado realmente curioso é a comparação de produção científica entre aqueles que conquistaram a Medalha Fields e aqueles que concorreram mas não ganharam. Basta ver o gráfico abaixo.
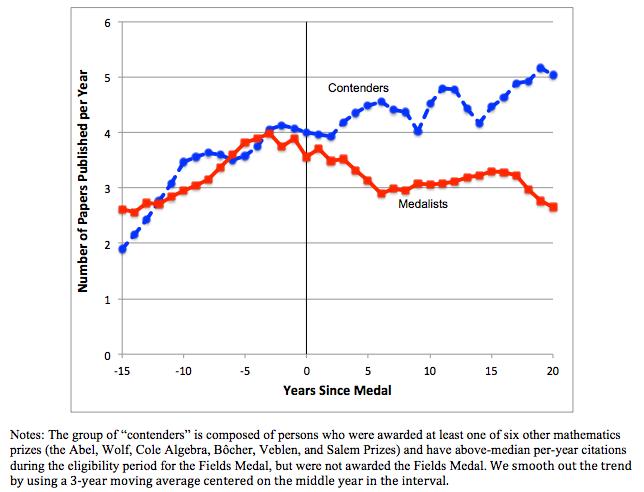
Enquanto a linha vermelha indica produção científica (somente em termos de quantia de publicações) de ganhadores da Medalha Fields, a linha azul corresponde à produção de concorrentes que não conquistaram esta honraria. Ou seja, a produção matemática de medalhistas cai em quantidade logo após o recebimento do prêmio, enquanto os demais aumentam a produção.
E quanto a impacto de pesquisas? De acordo com Borjas e Doran, medalhistas Fields apresentam uma média de 64 citações ao ano, enquanto concorrentes não contemplados apresentam uma média de 56 citações ao ano. Portanto, a diferença é pequena e certamente carrega em si o prestígio social da Medalha Fields. Em termos de impacto, ambas as categorias estão muito acima da média de 2,5 citações ao ano, no universo de 72 mil matemáticos existentes no mundo, de acordo com parâmetros acima citados da American Mathematical Society.
Outra informação relevante levantada por Borjas e Doran é a identificação de matemáticos que transformaram completamente esta ciência e que não foram contemplados pela Medalha Fields. Exemplos bem conhecidos são George Lusztig e John Tate, entre muitos outros. Há pelo menos quatro fatores arbitrários que justificam este fenômeno: o intervalo de quatro anos entre uma premiação e a próxima, a limitação de premiação para quatro matemáticos (no máximo), a restrição de idade (indivíduos com mais de 40 anos de idade não podem concorrer) e tendências de valorização de certas áreas da matemática em detrimento de outras. Segundo Borjas e Doran, os matemáticos contemplados pela Medalha Fields fizeram contribuições que não cobrem sequer metade das grandes conquistas matemáticas realizadas nos últimos 80 anos.
Naturalmente existem muitas outras formas de reconhecimento de mérito de pesquisa. Mas, em matemática, nenhum outro prêmio é tão impactante do ponto de vista social quanto a Medalha Fields.
Mas voltemos agora à questão de queda de produção e o que isso tem a ver com o título da postagem.
Sabendo que a conquista do Prêmio Nobel em Economia não altera de forma alguma a produtividade dos contemplados, fica então uma questão: por que a produção científica de matemáticos ganhadores da Medalha Fields diminui?
De acordo com o artigo de Borjas e Doran, ocorre um bizarro fenômeno comportamental entre ganhadores da Medalha Fields. Existe uma forte tendência para esses matemáticos migrarem seus interesses intelectuais para áreas do conhecimento não exploradas antes da conquista do prêmio. Pelo menos metade da queda de produção pode ser atribuída a esta propensão à experimentação.
Ou seja, a Medalha Fields serve de estímulo para o contemplado investir em futuras pesquisas? A resposta é positiva se olharmos do ponto de vista de uma necessidade individual de exploração de novos territórios. A resposta é negativa se olharmos do ponto de vista de pesquisas anteriormente realizadas.
A Medalha Fields serve de estímulo para os concorrentes não contemplados? A resposta é negativa se olharmos do ponto de vista de uma necessidade individual de exploração de novos territórios. A resposta é positiva se analisarmos do ponto de vista de um senso de continuidade de pesquisas anteriormente realizadas.
Portanto, examinemos outros dois pontos de vista: o institucional e o social.
Artur Ávila foi o primeiro brasileiro a conquistar a Medalha Fields. E ele conta com um vínculo no Instituto Nacional de Matemática Pura e Aplicada (IMPA), no Rio de Janeiro. Analisando os resultados de Borjas e Doran, fica claro que os principais beneficiados por esta conquista são o IMPA e o Brasil. Por quê? Porque esta conquista definitivamente impulsiona outros jovens matemáticos a buscar as grandes conquistas.
Para o indivíduo não deve fazer tanta diferença assim se ele ganha a Medalha Fields ou o Prêmio Nobel. Esta preocupação deve ser prioritariamente institucional e social. Instituições e segmentos sociais devem sim fazer campanhas internacionais para indicar seus mais brilhantes pesquisadores para fins de premiação, como fez o IMPA em várias ocasiões. Este incentivo exerce poderosa influência sobre muito mais gente do que apenas uma pessoa indicada.
Se matemáticos contemplados pela Medalha Fields demonstram interesses diferentes após a premiação, isso parece revelar um perfil psicológico que não ocorre em outras áreas do saber, como economia. E certamente é algo que deve ser melhor investigado e compreendido. O que há de diferente entre matemáticos? Ou será que o limitante de idade da Medalha Fields exerce uma influência que não atinge cientistas mais experientes?
O Brasil é um país que já tem um extenso histórico de desprezo por grandes pensadores que aqui nasceram e trabalharam. A conquista da Medalha Fields por um brasileiro, notícia quente ontem e fria hoje, é um sinal de que este perfil social pode mudar. Indivíduos são importantes sim, mas eles nada seriam sem um meio social que os estimule. Que o Brasil aprenda mais com o exemplo do IMPA e que o IMPA aprenda mais com os resultados de Borjas e Doran. Ninguém está imune à crítica.
- Matemáticos Lentos
O mais importante prêmio em matemática é a Medalha Fields. Mas, diferentemente do Prêmio Nobel, que abrange áreas científicas como medicina, física e química, a Medalha Fields tem um limitante de idade. Esta premiação jamais pode ser entregue...
- Deus E A Lógica Do Cnpq
Está agendado para o período de 1.o a 5 de abril deste ano o Primeiro Congresso Mundial Sobre Lógica e Religião, organizado por Jean-Yves Béziau, Itala D'Ottaviano e pela colaboradora do blog Matemática e Sociedade Maria Espindola, entre outros....
- Sobre Entrevista De Artur Avila No Programa De Jô Soares
O texto abaixo é de autoria de Maria Lewtchuk Espindola, física que trabalha no Departamento de Matemática da Universidade Federal da Paraíba (UFPB). O que ela escreve é motivado por uma entrevista recentemente concedida pelo matemático Artur Avila,...
- O Efeito De Elogios Sobre O Intelecto De Crianças
Este blog já existe há algum tempo. E frequentemente tenho insistido sobre a importância da família no processo educacional de jovens e crianças. No entanto, pouco tenho detalhado sobre o tema. Por conta disso, preciso remediar esta falha. Já publiquei...
- Fundamentos Da Ciência E Fator De Impacto
Tanto pesquisadores e cientistas quanto editores de periódicos científicos frequentemente fazem uma distinção entre ciência e fundamentos da ciência. Nem sempre essa distinção é promovida de forma explícita ou sequer consciente. Mas certamente...
Educação
Quem é realmente beneficiado pela Medalha Fields?

Em documento redigido no dia 12 de janeiro de 1932, o canadense John Charles Fields propôs que "duas medalhas de ouro sejam entregues por ocasião de sucessivos Congressos Internacionais de Matemática, como forma de reconhecimento de conquistas significativas em matemática. Por conta da multiplicidade de ramos desta área e levando em conta o fato de que o intervalo entre tais congressos é de quatro anos, pelo menos duas medalhas deveriam ser entregues." Fields ainda complementa seu documento, afirmando que esta medalha não deveria ser apenas um reconhecimento de trabalho já realizado, mas também "um encorajamento para o ganhador investir em pesquisas futuras, bem como um estímulo para o esforço renovado dos demais."
Pois bem. A primeira Medalha Fields, hoje reconhecida como o mais importante prêmio em matemática, foi outorgada em 1936 para Lars Ahlfors (Finlândia) e Jesse Douglas (Estados Unidos). A última foi concedida este ano para Maryam Mirzakhani (Irã), Martin Hairer (Áustria), Manjul Bhargava (Canadá, Estados Unidos) e Artur Ávila (Brasil, França). Ao longo de 78 anos de premiação para 56 matemáticos de 21 países (Finlândia, Estados Unidos, França, Noruega, Japão, Reino Unido, Suécia, Rússia, Itália, Bélgica, China, Alemanha, Ucrânia, Nova Zelândia, África do Sul, Austrália, Israel, Vietnã, Áustria, Irã e Brasil), o que se pode dizer sobre os sonhos de John Charles Fields? A Medalha Fields cumpre com o papel idealizado pelo seu criador? Esta é uma daquelas perguntas que não se responde com um simples sim ou não.
Em artigo a ser publicado em 2015 no periódico Journal of Human Resources, George J. Borjas (Harvard University) e Kirk B. Doran (University of Notre Dame) promovem uma detalhada análise do impacto da Medalha Fields sobre aqueles que conquistaram este importante prêmio. Para o leitor interessado em uma versão preliminar deste artigo, basta clicar aqui.
As conclusões de Borjas e Doran certamente abrem espaço para discussões aprofundadas até mesmo sobre os méritos da meritocracia. Daí a importância deste artigo. Estes autores avaliaram a produtividade científica de um universo de 72 mil matemáticos espalhados pelo mundo, de acordo com banco de dados da American Mathematical Society, que leva em conta profissionais com pelo menos vinte anos de experiência.
Por um lado, a média de produção científica de matemáticos é inferior a 32 artigos durante toda a carreira. Por outro lado, medalhistas Fields publicam acima de 116 artigos durante a vida profissional. Mas, curiosamente, os matemáticos concorrentes que não conquistaram este prêmio apresentam uma produção média ligeiramente superior, com 126 artigos. Até aí, esses números pouco revelam. O resultado realmente curioso é a comparação de produção científica entre aqueles que conquistaram a Medalha Fields e aqueles que concorreram mas não ganharam. Basta ver o gráfico abaixo.

Enquanto a linha vermelha indica produção científica (somente em termos de quantia de publicações) de ganhadores da Medalha Fields, a linha azul corresponde à produção de concorrentes que não conquistaram esta honraria. Ou seja, a produção matemática de medalhistas cai em quantidade logo após o recebimento do prêmio, enquanto os demais aumentam a produção.
E quanto a impacto de pesquisas? De acordo com Borjas e Doran, medalhistas Fields apresentam uma média de 64 citações ao ano, enquanto concorrentes não contemplados apresentam uma média de 56 citações ao ano. Portanto, a diferença é pequena e certamente carrega em si o prestígio social da Medalha Fields. Em termos de impacto, ambas as categorias estão muito acima da média de 2,5 citações ao ano, no universo de 72 mil matemáticos existentes no mundo, de acordo com parâmetros acima citados da American Mathematical Society.
Outra informação relevante levantada por Borjas e Doran é a identificação de matemáticos que transformaram completamente esta ciência e que não foram contemplados pela Medalha Fields. Exemplos bem conhecidos são George Lusztig e John Tate, entre muitos outros. Há pelo menos quatro fatores arbitrários que justificam este fenômeno: o intervalo de quatro anos entre uma premiação e a próxima, a limitação de premiação para quatro matemáticos (no máximo), a restrição de idade (indivíduos com mais de 40 anos de idade não podem concorrer) e tendências de valorização de certas áreas da matemática em detrimento de outras. Segundo Borjas e Doran, os matemáticos contemplados pela Medalha Fields fizeram contribuições que não cobrem sequer metade das grandes conquistas matemáticas realizadas nos últimos 80 anos.
Naturalmente existem muitas outras formas de reconhecimento de mérito de pesquisa. Mas, em matemática, nenhum outro prêmio é tão impactante do ponto de vista social quanto a Medalha Fields.
Mas voltemos agora à questão de queda de produção e o que isso tem a ver com o título da postagem.
Sabendo que a conquista do Prêmio Nobel em Economia não altera de forma alguma a produtividade dos contemplados, fica então uma questão: por que a produção científica de matemáticos ganhadores da Medalha Fields diminui?
De acordo com o artigo de Borjas e Doran, ocorre um bizarro fenômeno comportamental entre ganhadores da Medalha Fields. Existe uma forte tendência para esses matemáticos migrarem seus interesses intelectuais para áreas do conhecimento não exploradas antes da conquista do prêmio. Pelo menos metade da queda de produção pode ser atribuída a esta propensão à experimentação.
Ou seja, a Medalha Fields serve de estímulo para o contemplado investir em futuras pesquisas? A resposta é positiva se olharmos do ponto de vista de uma necessidade individual de exploração de novos territórios. A resposta é negativa se olharmos do ponto de vista de pesquisas anteriormente realizadas.
A Medalha Fields serve de estímulo para os concorrentes não contemplados? A resposta é negativa se olharmos do ponto de vista de uma necessidade individual de exploração de novos territórios. A resposta é positiva se analisarmos do ponto de vista de um senso de continuidade de pesquisas anteriormente realizadas.
Portanto, examinemos outros dois pontos de vista: o institucional e o social.
Artur Ávila foi o primeiro brasileiro a conquistar a Medalha Fields. E ele conta com um vínculo no Instituto Nacional de Matemática Pura e Aplicada (IMPA), no Rio de Janeiro. Analisando os resultados de Borjas e Doran, fica claro que os principais beneficiados por esta conquista são o IMPA e o Brasil. Por quê? Porque esta conquista definitivamente impulsiona outros jovens matemáticos a buscar as grandes conquistas.
Para o indivíduo não deve fazer tanta diferença assim se ele ganha a Medalha Fields ou o Prêmio Nobel. Esta preocupação deve ser prioritariamente institucional e social. Instituições e segmentos sociais devem sim fazer campanhas internacionais para indicar seus mais brilhantes pesquisadores para fins de premiação, como fez o IMPA em várias ocasiões. Este incentivo exerce poderosa influência sobre muito mais gente do que apenas uma pessoa indicada.
Se matemáticos contemplados pela Medalha Fields demonstram interesses diferentes após a premiação, isso parece revelar um perfil psicológico que não ocorre em outras áreas do saber, como economia. E certamente é algo que deve ser melhor investigado e compreendido. O que há de diferente entre matemáticos? Ou será que o limitante de idade da Medalha Fields exerce uma influência que não atinge cientistas mais experientes?
O Brasil é um país que já tem um extenso histórico de desprezo por grandes pensadores que aqui nasceram e trabalharam. A conquista da Medalha Fields por um brasileiro, notícia quente ontem e fria hoje, é um sinal de que este perfil social pode mudar. Indivíduos são importantes sim, mas eles nada seriam sem um meio social que os estimule. Que o Brasil aprenda mais com o exemplo do IMPA e que o IMPA aprenda mais com os resultados de Borjas e Doran. Ninguém está imune à crítica.
loading...
- Matemáticos Lentos
O mais importante prêmio em matemática é a Medalha Fields. Mas, diferentemente do Prêmio Nobel, que abrange áreas científicas como medicina, física e química, a Medalha Fields tem um limitante de idade. Esta premiação jamais pode ser entregue...
- Deus E A Lógica Do Cnpq
Está agendado para o período de 1.o a 5 de abril deste ano o Primeiro Congresso Mundial Sobre Lógica e Religião, organizado por Jean-Yves Béziau, Itala D'Ottaviano e pela colaboradora do blog Matemática e Sociedade Maria Espindola, entre outros....
- Sobre Entrevista De Artur Avila No Programa De Jô Soares
O texto abaixo é de autoria de Maria Lewtchuk Espindola, física que trabalha no Departamento de Matemática da Universidade Federal da Paraíba (UFPB). O que ela escreve é motivado por uma entrevista recentemente concedida pelo matemático Artur Avila,...
- O Efeito De Elogios Sobre O Intelecto De Crianças
Este blog já existe há algum tempo. E frequentemente tenho insistido sobre a importância da família no processo educacional de jovens e crianças. No entanto, pouco tenho detalhado sobre o tema. Por conta disso, preciso remediar esta falha. Já publiquei...
- Fundamentos Da Ciência E Fator De Impacto
Tanto pesquisadores e cientistas quanto editores de periódicos científicos frequentemente fazem uma distinção entre ciência e fundamentos da ciência. Nem sempre essa distinção é promovida de forma explícita ou sequer consciente. Mas certamente...
